Create accountLogin

Recent searches

No recent searches

Search options

Only available when logged in.
ohai.social is one of the many independent Mastodon servers you can use to participate in the fediverse.
A cozy, fast and secure Mastodon server where everyone is welcome. Run by the folks at ohai.is.

Administered by:

Server stats:

1.8K
active users

ohai.social: AboutStatusProfiles directoryPrivacy policy

Mastodon: AboutGet the appKeyboard shortcutsView source codev4.4.0-nightly.2025-04-01

#navierstokes

0 posts0 participants0 posts today
Public *
Pustam | पुस्तम | পুস্তম🇳🇵

An Article in the Annual Review of Condensed Matter Physics on Turbulence by KR Sreenivasan and J Schumacher
annualreviews.org/content/jour

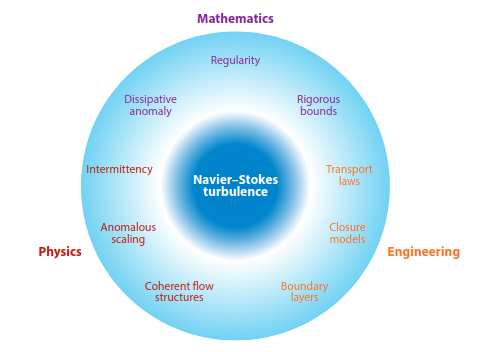
What is the turbulence problem, and when can we say it’s solved? 🌪️ This deep dive by Sreenivasan & Schumacher explores the math, physics, and engineering challenges of turbulence—from Navier-Stokes equations to intermittency and beyond. A must-read for anyone fascinated by chaos, complexity, and the unsolved mysteries of fluid dynamics! 🌀

A summary of the talk presented by KR Sreenivasan in December 2023 at the International Center for Theoretical Sciences (ICTS-TIFR) in Bengaluru, as part of a program on field theory and turbulence.
youtube.com/watch?v=fwVSBYh-KC

"Field Theory and Turbulence" program link: icts.res.in/discussion-meeting

#FluidDynamics #Physics #NavierStokes #UnsolvedMystery #Mechanics #Dynamics #FluidMechanics #Science #Chaos #TurbulentMotion #Randomness #Chaotic #Fluid #ClassicalMechanics
#Turbulence

Continued thread
Public
Giuseppe Bilotta

So, I mentioned already that we cannot really model #lava flows. The main reasons for that is that we don't actually know how lava behaves, at least not in sufficient detail.

Of course, lava is a fluid, and a (very) viscous one at that, so we know that it follows the Navier–Stokes equations. We also know that its behavior is heavily dependent on temperature, so we know that we also need the heat equation, with both kinds of boundary conditions (conduction to ground, and radiation on the free surface).

And that's all we know. Seriously.

OK, not really, but everything else is extremely uncertain. When modeling a viscous fluid (like lava, or any other geophysical flow for the matter), the first thing you need to know is what the viscosity is. And for lava, we don't know. There's a lot of things we do know, but not enough.
For example, we know that the viscosity depends on temperature, chemical composition, degree of crystalization, amount and types of volatiles in the melt, and so on and so forth. But we don't exactly know the laws relating the viscosity to all of these chemical and physical properties.

2/

#NavierStokes#NavierStokesEquations
Public
Chapel Programming Language

In the concluding article of his "Navier-Stokes in Chapel" series, Jeremiah Corrado demonstrates how a Chapel program with size and complexity like Python performs and scales competitively with a more complex C++/MPI/OpenMP port.

chapel-lang.org/blog/posts/bns

Thanks to the @labarba group for creating and maintaining the CFD Python tutorials upon which this series was based! lorenabarba.com/blog/cfd-pytho

Screen shot of the linked blog article
A quiver flow plot and pressure gradient. These images are the results of running a fluid dynamics simulation written in Chapel.
A graph comparing the time to run the Chapel and C++ versions as the number of nodes is increased. The Chapel version is competitive with the C++ version and it's actually faster for the larger problem size.
#ChapelLang#CFD#NavierStokes
Public
FluidDyn

#ThisMonthInFluiddyn it is. Let's go 😎

🔹@PierreAugier and friends are finishing up an article, so as a side project they released #formattex and #formatbibtex based on #TexSoup and #BibtexParser

pypi.org/project/formattex/
pypi.org/project/formatbibtex/

> a simple and uncompromising #Latex code formatter

🔹Version 0.7.4 of #fluidsim and fluidsim-core were released containing a refactored energy spectra for #NavierStokes solvers and other bug fixes

pypi.org/project/fluidsim/

PyPIformattexA simple and uncompromising Latex code formatter
#fluiddyn
Public *
Greg Yang

Learned a lot from my lunch with Thomas Hou today, who recently finally vindicated his 10 year quest of showing the (axisymmetric, incompressible) Euler equation blows up. arxiv.org/abs/2210.07191
#PDE #NavierStokes #Euler #Math #Physics #MachineLearning #DeepLearning

arXiv.orgStable nearly self-similar blowup of the 2D Boussinesq and 3D Euler equations with smooth dataInspired by the numerical evidence of a potential 3D Euler singularity [Luo-Hou-14a, Luo-Hou-14b], we prove finite time blowup of the 2D Boussinesq and 3D axisymmetric Euler equations with smooth initial data of finite energy and boundary. There are several essential difficulties in proving finite time blowup of 3D Euler with smooth initial data. One of the essential difficulties is to control a number of nonlocal terms that do not seem to offer any damping effect. Another essential difficulty is that the strong advection normal to the boundary introduces a large growth factor for the perturbation if we use weighted $L^2$ estimates. We overcome this difficulty by using a combination of a weighted $L^\infty$ norm and a weighted $C^{1/2}$ norm, and develop sharp functional inequalities using the symmetry properties of the kernels and some techniques from optimal transport. Moreover we decompose the linearized operator into a leading order operator plus a finite rank operator. The leading order operator is designed in such a way that we can obtain sharp stability estimates. The contribution from the finite rank operator can be captured by an auxiliary variable and its contribution to linear stability can be estimated by constructing approximate solution in space-time. This enables us to establish nonlinear stability of the approximate self-similar profile and prove stable nearly self-similar blowup of the 2D Boussinesq and 3D Euler equations with smooth initial data and boundary.
ExploreLive feeds
About